The main issue to be
tackled in
the design of or-parallel systems is the development of an effective environment
representation scheme, capable of associating to each or-branch the correct set
of variable bindings. The two main approaches commonly used to solve this
problem are stack-copying and binding arrays![]() .
.
Stack-Copying: the stack-copying approach is characterized by a very intense memory usage. Since each or-agent has a whole copy of its branch, the same information appears repeated over and over in the stacks of different agents. Furthermore, in order to avoid repetition of computation, for each choice point belonging to the shared part of the tree (i.e., the part of the tree that has been copied by different agents) a shared frame has to be created, which stores information that are required by all the agents working on such choice-points (e.g., which are the alternatives still unexplored). Various issues can be raised regarding this model.
The first natural question is whether there is really the need of performing this large amount of copying. Copying involves all the data areas of the abstract machine (choice-point stack, environment stack, heap, and trail)--which translates to a considerable overhead during execution, considering also that during the copying operation both the agents involved (the agent copying and the agent the information are copied from) need to suspend their normal activity. Muse [4], the first system which introduced stack-copying, tries to improve the situation by:
On the other hand it seems intuitively possible to do better than this. Having distinct copies of certain data structures, like choice points, does not seem to have much sense, especially considering the fact that additional data structures (the shared frames) need to be introduced to create connections between the different copies of the same entity. On the other hand, sharing data structures which can be subject to updates during the execution can have the side effect of requiring mutual exclusion during accesses--which may become itself a source of overhead. It seems anyway possible to improve the situation by finding a proper compromise, in which information that are seldomly updated (e.g., choice points) are shared between computations, while those that either must be kept independent (e.g., conditional bindings) or are subject of frequent updates (e.g. trail) are duplicated. This can be interpreted as an intermediate point between two extremes, where one extreme is constituted by pure stack-copying and the other by pure sharing (e.g., Binding Arrays).
Garbage Collection is another complex issue in stack-copying. This may not be very apparent, since thanks to stack-copying the different agents can apply a standard WAM-like behaviour, carrying out local garbage collection on their own stacks. On the other hand, one of the key elements in the efficient implementation of stack-copying is the incrementality of the process: copying of the common state of the two agents is avoided. But if one of the two agents has performed garbage collection then finding out the common part of the two agents' state becomes very difficult. One possibility is to simply get rid of incremental copying in case of modification of the state due to garbage collection--quite undesirable due to the large amount of data that may be copied. Alternatively, new garbage collection mechanisms need to be introduced, which fit in a better way in the stack-copying model (e.g. the segmented garbage collection mechanism used by Muse).
Binding Arrays: the Binding Arrays (B.A.) approach represents the symmetrical approach w.r.t. stack-copying regarding the amount of copying/sharing involved. In B.A. the maximal amount of sharing is enforced between the different agents. The only component should be kept separate across the different agents is the set of bindings to the conditional variables, which are kept in the private binding array of each agent. When one agent starts a new computation, it needs to perform a ``copy'' of the binding array in order to update its local state.
Various issues related to memory management emerge in the B.A. approach. First of all, the binding arrays need to be maintained in such a way to allow an efficient management. In the implementation of Aurora each agent is maintaining a local binding array which is updated whenever a new computation is started. Recent experiences by the group of Vitor Santos Costa [19] have shown that using a unique binding array shared by the different agents may lead to improvements and various optimizations. This issue may become of fundamental importance when dealing with and/or-parallel systems (as described later on).
Furthermore, the current approach in updating the binding arrays consists of scanning the trail of the agent from which work is going to be taken, in order to detect the bindings that are missing from the current state. This can become quite time consuming--different techniques should be considered, like transforming this phase into a real ``copying'' operation, which can be performed quickly and holding the two agents synchronized for a shorter period of time.
Another problem related to memory management in the B.A. approach is garbage collection on the shared areas. Let us consider the situation exemplified in figure 13.
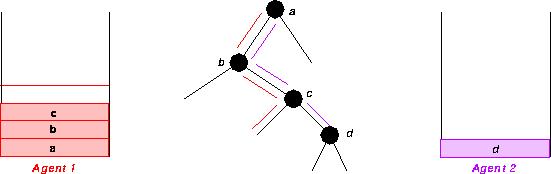
Figure 13: Garbage Collection in Binding Array
If Agent 1 backtracks over choice point c, it will not be allowed to reclaim space, since the same choice point is still needed by Agent 2. Agent 1 will be forced to allocate new data structures on the top of its stack, over c. If successively also Agent 2 backtracks, node c may become useless and a gap in Agent 1's stack will remain--this is called ghost node in Aurora's terminology. These gaps should be properly marked and recovered upon backtracking.