Memory Management in And-Parallelism

  As mentioned above, memory management becomes extremely complex in presence of and-parallelism, as illustrated in various works [97, 83, 59]. The original proposals (e.g., RAPWAM [58, 118]) were based on memory management schemes which were trying to mimic as close as possible memory management of the WAM. In particular, restrictions were imposed on the and-scheduler in order to maintain in the stacks the ``correct'' order--i.e., topmost objects on the stacks should be those that are going to be reclaimed first on backtracking. This, as illustrated from various experimental results [97], was leading to severe restrictions on the amount of parallelism exploited.

More recent models [94, 46] relax this restrictions, at the cost of more complex memory management schemes. And this cost becomes evident both in terms of memory consumption (more data structures are required in order to maintain the correspondence between physical and logical layout of the computation), and in terms of overhead (allocation, initialization, traversal, and removal of the new data structures). The impact on the global efficiency can be considerable. Techniques have been studied to reduce these overheads [83]. Furthermore, new models for and-parallelism are currently under considerations, where most of these additional operations are avoided, with the only drawback of having to introduce an explicit garbage collector.

In the rest of this section we will discuss the two main aspects related to memory management in and-parallel systems: representation of environments and trail management.

Goal Stacking vs. Environment Stacking

Since the earlier designs of Prolog engines, the implementors debated about the best machine organization to adopt in order to support the control behaviour of a Prolog execution. Prolog execution is essentially characterized by two phases:

1. Forward Execution: which corresponds to the application of SLD-resolution and the computation of the succession of resolvents of the initial query (management of don't care nondeterminism);
2. Backward Execution: which corresponds to the management of don't know nondeterminism--the set of mechanisms invoked upon occurrence of a failure in the current execution.

While the management of don't know nondeterminism is quite well-established, through the use of choice-points allocated on a proper control stack, the management of forward execution leaves various alternatives open. In particular, two major approaches have been considered and are currently used in various implementations:

1. Environment Stacking: this is the model which has been assumed in the previous sections. An environment is allocated whenever a clause is entered, and used to maintain a (fairly implicit) representation of the current goals chain and to maintain the local environment of the clause.

   Environment stacking has various advantages and appears to properly model the sequential pattern of execution. The use of environments guarantees a compact representation of forward execution, and allows incremental refinements of the environment during the execution (through environment trimming, a technique which allows to drop from the environment local variables which are not needed anymore).

2. Goal Stacking: in goal stacking, the system maintains an explicit representation of the goal list generated during the successive steps of resolution. The engine manipulates a goal stack. Each subgoal is represented by a data structure allocated in this stack and, at each moment, the current resolvent is represented by the succession of data structures present in the goal stack. In principle, no environments are created for the clauses, while each subgoal has its own arguments directly associated.

   Goal stacking has various advantages, like:

   1. by making explicit the structure of the current resolvent, it offers a more precise view of the status of the execution, which can be used for various purposes (e.g., it makes easier to implement different selection strategies);
   2. various optimizations can be applied more naturally (e.g., tail recursion optimization).
   3. as pointed out by Warren [116], goal stacking reduces the number of jumps in the code (good for pipelined architectures) and improves locality of the accesses to the code (reducing memory page faults).

   On the other hand, goal stacking suffers of some drawbacks:

   1. all the subgoals need to be created upon entering a clause--this work can get wasted in case of an early failure in the clause;
   2. variables management becomes more complex. In particular for unbound variables--either frequent run-time checks are required to avoid dangling references or all of them need to be globalized (e.g., allocated on the heap), increasing memory consumption and making garbage collection more complex.

In most of the current sequential implementations, environment stacking has been preferred to goal stacking--this especially in view of the best management of variables offered.

On the other hand, switching to parallelism, and more specifically to and-parallelism, the situation becomes more complex. What is evident is that environment stacking becomes an obstacle in the exploitation of and-parallelism. First of all, and-parallelism requires the availability of an explicit representation of the resolvent (or, at least, of the part of the resolvent that is meant to be executed in and-parallel), in order to allow the various and-agents to identify the parallel work available, and take advantage of it. Using environment stacking, the structure of the resolvent is implicit in the code addresses stored in the environments and in the code itself--making the task of identifying the successive subgoals extremely hard and costly.

To gain efficiency, and-parallel systems need to introduce, at least up to a certain extent, a form of goal-stacking. Systems like ACE, &-Prolog, DDAS, APEX limit the introduction of goal stacking to those subgoals which can potentially be executed in parallel, while maintaining environment stacking to represent clauses' local environments and the sequential parts of the resolvent. Other systems, like the parallel implementation of Parlog [23], extend the use of goal stacking to the whole execution. In various other systems (e.g. DDAS and CIAO Prolog [54]) the lack of an explicit goal chain representation leads to the need of recreating the sequence of subgoals through the use of special data structures properly linked--this is necessary to support the correct backtracking semantics. Nevertheless, the cost of maintaining these additional data structures (creation, update, traversal) seriously endangers the efficiency of the parallel execution, leading to actual slow downs for programs with particular execution behaviours (e.g., programs with heavy backtracking).

Management of the Trail

Even though memory management has been shown to be an important issue, it is opinion of the author that, as long as the implementation does not lead to a combinatorial explosion in memory consumption, efficiency of execution should not be sacrificed to reduce memory consumption or facilitate garbage collection. This is particularly true when dealing with parallel systems where

• overheads are introduced to support parallel execution;
• memory management becomes very complex--and, as a consequence, the techniques to recover memory and recollect garbage become more and more expensive.

When dealing with and-parallel systems, recovering memory upon backtracking is an awkward task. Backtracking can be realized in two different ways:

(i). Private Backtracking: each and-agent is allowed to backtrack only over the parts of the computation that it has generated. Let us consider the scenario in which a query of the form a & b & c is given, the agent has executed a and c, while agent has computed b. Assuming the use of a recomputation-based approach, backtracking will move from c, to b, and finally to a. will start the backtracking activity, but it will stop once all the alternatives of c have been exhausted--not being allowed to backtrack over b, which is owned by . Backtracking needs to be transferred to .

This approach allows an easier recovery of memory (the agent backtracking owns the data structures, which can be immediately recollected), and it has been used in various systems, like the original &-Prolog and a preliminary version of ACE. On the other hand, the price paid for having an easier memory management is a considerably lack of efficiency during backtracking. Backtracking is not anymore a continuous activity, but is a sequence of sequential steps performed by different agents, with all the expenses incurred to ensure a proper synchronization and transfer of control.

(ii). Public Backtracking: every agent is allowed to backtrack over any memory area, independently from the actual owner. In the example above, if a new alternative is located in b, then the agent will backtrack to it, even if b is owned by . This method requires care in order to avoid conflicts (due to different agents backtracking on the same area)--which can be realized by adding simple locks and runtime checks upon failure. But, on the other hand, one agent will complete the whole backtracking, without any synchronization activity and without transferring the backtracking task between agents (as was happening in private backtracking). This makes the whole backtracking much faster (figure 12 shows an estimated comparison of speedups obtained using the two forms of backtracking).

  
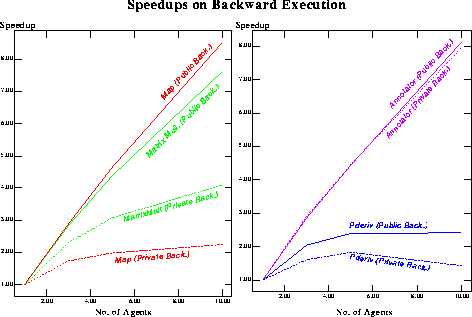
Figure 12: Comparison of Public and Private Backtracking.

The main disadvantage of public backtracking is the inability of performing garbage collection on the fly during backtracking--clearly an agent cannot recover memory belonging to another agent. On the other hand areas to be reclaimed can be marked during backtracking, and recovered in a successive, separate garbage collection phase.

The current version of ACE, and other systems, like DDAS, are based on this backtracking scheme.

The discussion above is useful to introduce another important issue in the implementation of and-parallelism. As we have seen, we can develop backtracking schemes where memory recovering is not affecting the system's efficiency. The natural question is then the following: which are the operations involved during backtracking that must be done and, on the other hand, which are those that can be avoided or delayed to a later stage of execution?

In the sequential models, backtracking represents the combination of the following activities:

• detection of unexplored alternatives in a choice point;
• detection of the backtracking points;
• removal of trailed bindings;
• recover of space on control stack, environment stack, and heap.

Of the four activities above, only three of them are strictly necessary, selection of backtracking points, extraction of alternatives, and removal of trailed bindings. While the first two steps can be realized efficiently and easily in an and-parallel system, the third point represents the main source of complexity on backtracking.

Identifying the bindings to be removed is straightforward in a sequential model, since there is a unique trail and there is a one-to-one correspondence between order of backtracking and order of the entries in the trail. This has the considerable advantage that, once the backtracking point has been detected, the set of bindings to be removed can be obtained in a single step--this thanks to the fact that a single piece of information is sufficient to detect the set of conditional bindings to remove.

The distributed nature of an and-parallel execution makes this whole process more complex: the trailed bindings are distributed in the trail stacks of the different agents, lacking the element that was allowing efficient untrailing in sequential system, i.e. the contiguity of the trailed bindings.

Most of the existing and-parallel systems use a memory organization similar to that of sequential systems, and are consequently obliged to explicitly compute at backtracking time the sequence of bindings to be removed. An improvement can be obtained by incrementally associating the parts of trail to the choice points, in such a way to facilitate their retrieval during backtracking.

Nevertheless, the perfect situation can be realized only by adopting a radically different memory organization, in which the contiguity of the trail is guaranteed. No models with this property have been proposed in the literature.