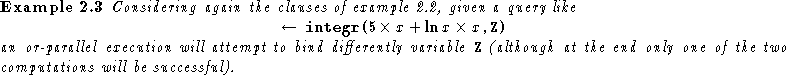Next: And-parallelism
Up: Or-parallelism
Previous: Restricted Or-Parallelism:
this represents the most general form of or-parallelism, in which no restrictions
are imposed a priori on the exploitation of parallelism.
This general form of or-parallelism requires, as described before, the development of
new environment representation techniques, in order to tackle the dependency problem in
the access and binding of conditional variables. During the execution of a resolution
step, new variables may be created (the variables local to the clause used in the resolution
step). Later on, the computation may split, due to the presence of or-parallelism, and the
different executions may clash in trying to read and/or write the variables created
in the ``shared'' part of the computation.
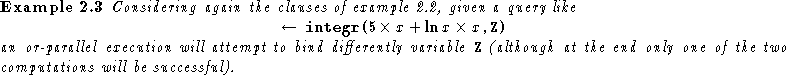
The environments should be organized in such a way that, in spite of the fact that
a part of the computation is ``shared'' (the part before the choice-point), the
correct bindings applicable to each branch are easily identifiable.
And this representation should be efficient, it should not add unbearable overheads.
The problem has
to be solved by devising a mechanism where each branch of the or-tree has some private
area, used to store the bindings to the conditional variables.
A variety of schemes have been proposed to tackle this problem ([40, 48]
present a thorough comparison of more than 20 models). They differ in the way in which
creation and access to these private areas are organized.
Of the many approaches proposed, two have been proved to be superior in terms of
efficiency and flexibility.
- Stack-copying: the environment representation problem is solved by
performing copies of the ``shared'' environments. Each branch of the or-tree owns
a private copy of all the environments (relevant to such branch), avoiding in such way any conflict in
binding conditional variables. Furthermore, with this technique the computation
carried on by each or-agent resembles exactly a standard sequential execution.
Figure 6(ii) illustrates this approach in the case of the query of
example 2.3. The first processor (on the left) generates a
choice point with unexplored alternatives; the second processor creates a local
copy of the computation up to such choice point (in particular, as illustrated in
the figure, the environments are duplicated) and continues with one of the
unexplored alternatives.
Efficiency can be achieved by making the environment
copying process an incremental activity.
This technique has been introduced for the first time
in the MUSE system [5, 4], and successively
adopted by other systems (e.g., ACE).
- Binding Arrays: in this scheme, an index is associated to each conditional variable,
and each branch has an associated array where bindings
to conditional variables will be stored. Whenever a conditional variable is
accessed, its index is used to identify an entry in the local binding array, where
the binding will be retrieved and/or stored. Whenever an or-agent starts executing
an alternative from a choice-point, it must update its binding array in order to
reflect the current state of the conditional variables. An example of use of
binding arrays, on the usual query of example 2.3, is shown in
figure 6(i). The variable Z is conditional and it is translated at
its creation time in a reference to entry 0 of the binding arrays. Each processor
will create the binding for Z in the entry 0 of its local binding array.
This technique has been
originally developed in the Aurora system [74], and successively adopted by other systems (e.g.,
Andorra-I).
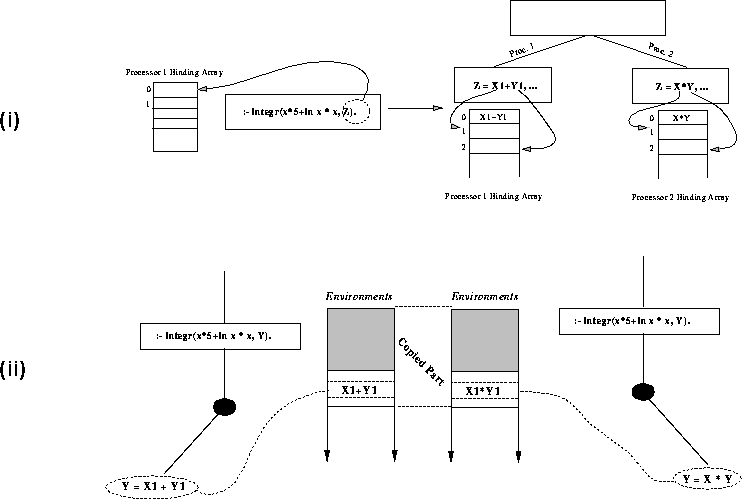
Figure 6: Stack-copying and Binding Arrays
Web Tour




Next: And-parallelism
Up: Or-parallelism
Previous: Restricted Or-Parallelism:
'Enrico
Tue Mar 19 14:37:09 MST 1996