Parallelism in Logic Programming

Logic Programming offers some unbeaten opportunities for implicit exploitation of parallelism. This is quite evident from the presentation of its operational semantics in the previous section. The resolution algorithm offers various degrees of non-determinacy, i.e. points of the execution where different alternatives are available to continue the computation. In any sequential implementation, these choices will be serialized--i.e. explored in some order (depending on the definition of the various selection operations). On the other hand, it is feasible to consider the possibility of exploring different alternatives concurrently, i.e., in parallel.

Furthermore, logic programming satisfies the second desired requirement--allowing natural ways to intervine on the exploitation of parallelism, e.g. through user annotations which do not ``disturb'' the structure of the program.

Various forms of parallelism can be exploited from logic programming languages, depending on which selection operations are transformed into ``parallel'' operations. It is custom to identify the following major forms of parallelism [18]:

1. Or-parallelism: Or-parallelism emerges from executing in parallel the different clauses that can be used to solve the selected subgoal. Intuitively, each subgoal can be solved by using different clauses (all those whose head unifies with the subgoal), and each of them gives rise to an alternative execution path. This can be depicted as a tree (the Or-tree), having a node for each selected subgoal and a branch for each clause matching the subgoal. Figure 2 illustrates an example of Or-tree (on the right).

     
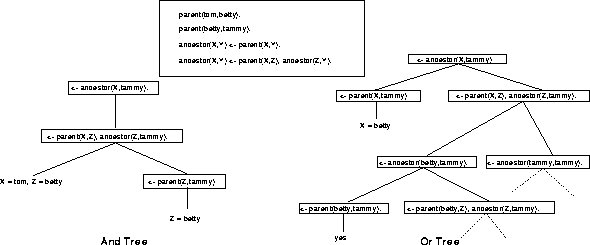
   Figure 2: And-tree and Or-tree
   

   In a sequential system the tree is visited in a predetermined order (e.g., in Prolog a left-to-right, depth-first search is used). Whenever a leaf of the tree is reached (a solution or a failure point) and a new solution is desired, a node with unexplored branches is selected and the new branch is traversed. This process is called backtracking. Nodes in an or-tree are usually named choice-points.

   In an or-parallel system different computing agents are concurrently exploring different branches of the or-tree.

2. And-parallelism: a dual view of a computation can be obtained by considering the non-determinism present in the subgoal selection operation. This can be described using a tree, the And-tree: each node represents (part of) a query and a node has a successor for each subgoal present in the query associated to such node. Figure 2 (on the left) illustrates an example of and-tree.

   In a sequential execution subgoals are selected one at the time from the current query--and the computation will stop when the query is empty or when a failure is encountered. This is equivalent to a traversal of the and-tree performed following a predefined order. And-parallelism is obtained by allowing the concurrent resolution of different subgoals of a given query--i.e., allowing different computing agents to explore different parts of the and-tree.

Other forms of parallelism (e.g. unification parallelism) have been identified but, due to their fine granularity, they require specialized architectures in order to achieve results of any interest. We will not be concerned with them in the rest of this work. A good source of information about unification parallelism is Jonas Barklund.