The Ria library algorithms

Arc consistency

Ria uses an arc consistency propagation algorithm. This terminates when all arcs are consistent, i.e. when for each variable, setting it to a value outside it's range would violate at least one constraint.

In a preprocessing step complex constraints are broken up into simple directed constraints. If necessary, auxiliary variables are introduced. For example:

X * (Y+Z) = 1

rewrites into

Aux  iis  Y + Z,
Z    iis  Aux - Y,
Y    iis  Aux - Z,
X    iis  1 / Aux,
Aux  iis  1 / X

Changes in the ranges of the input variables (right hand side) trigger the constraints to recompute the range for the output variable (left hand side).

At any time several constraints may be triggered. A heuristic favouring constraints that have been succesful at trimming variable ranges in the past is used for selection of the next constraint to compute.

Arc consistency threshold

If the execution of a constraint, restricts the range of a variable by a quantity less than the propagation threshold, this restriction is simply not applied. This terminates propagation early and prevents almost infinite loops of ever tinier propagations on ill-behaved problems. For example:

[eclipse 17]: set_threshold(1e-3).

yes.
[eclipse 18]: ria:(sin(X) =:= X).

X = X{-0.18143335721992979 .. 0.18143335721992984}
yes.
[eclipse 19]: Y is 0.18143335721992981 - sin(0.18143335721992981).

Y = 0.00099376872589851394
yes.

For small X X and sin(X) are almost identical, the library in this case will have made two variables and two directed constraints out of the above example.

These are:

sin(X) -> S
arcsin(S) -> X

Since each propagation only makes tiny differences to the domains of S and X the algorithm stops.

Intuitively this slowly convergent behaviour happens when the solution is a point where two curves meet at a tangent.

Squash algorithm

A stronger propagation algorithm is also included. This is built upon the normal arc consistency. It guarantees that, if you take any variable and restrict its range to a small domain near one of its bounds, the original arc consistency solver will not find any constraint unsatisfied.

Figure 5.1: Propagation with Squash algorithm (example)

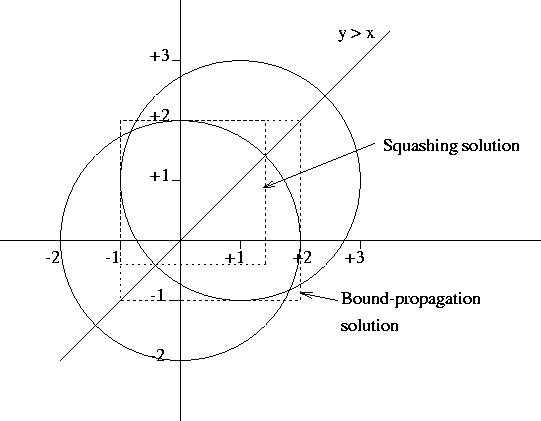
All points (X,Y) Y >= X, lying within the intersection of 2 circles with radius 2, one centred at (0,0) the other at (1,1).

[eclipse 29]: ria:(4 >= X^2 + Y^2), ria:(4 >= (X-1)^2+(Y-1)^2), ria:(Y >= X).

Y = Y{-1.0000000000000016 .. 2.0000000000000013}
X = X{-1.0000000000000016 .. 2.0000000000000013}
yes.

The arc-consistency solution does not take into account the X >= Y constraint. Intuitively this is because it passes through the corners of the box denoting the solution to the problem of simply intersecting the two circles.

[eclipse 29]: ria:(4 >= X^2 + Y^2), ria:(4 >= (X-1)^2+(Y-1)^2), 
		ria:(Y >= X), squash([X,Y],1e-5,lin).

X = X{-1.0000000000000016 .. 1.4142135999632603}
Y = Y{-0.41421359996326074 .. 2.0000000000000013}
yes.