

Next: Other methods
Up: Statistical Inference
Previous: Statistical Inference
Bayesian networks are a popular way for representing probabilistic
knowledge in artificial intelligence. They have been used for quite
some time [37,29], but their use was
restricted until the late eighties due to efficiency reasons. Work by
Pearl [93] and Lauritzen and Spiegelhalter
[71] on efficient localized
interpretation methods led to the renewed interest in Bayesian
networks.
Pearl [92,93] has done influential work on
probabilistic reasoning for artificial intelligence. An important
contribution is a method for localized computation of Bayesian
networks for the special case of polytrees (singly connected
networks). This is done by breaking down the probabilistic support
for a node into two components. The first component is the causal
support from the node's parents (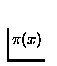 ), potentially influenced by
other children of the parents. The other component is the influence
from the node's childrens (
), potentially influenced by
other children of the parents. The other component is the influence
from the node's childrens (
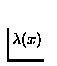 ). By separating these
components, belief propagation can be done locally without introducing
instabilities (e.g., counting evidence twice).
). By separating these
components, belief propagation can be done locally without introducing
instabilities (e.g., counting evidence twice).
Lauritzen and Spiegelhalter [71]
also have done influential work in improving the efficiency of
Bayesian Networks. They describe a method that can be used for any
type of Bayesian Networks, not just polytrees as above. The idea is to
convert the directed graph into a tree of cliques, where each clique
is a maximal set of nodes that directly influence each other.
Propagation then proceeds among the cliques in a manner analogous to
that in Pearl's method.
Many commercial systems for Bayesian Networks incorporate this
algorithm. In particular, this algorithm forms the basis for the
belief propagation in Hugin [62] which was developed by
researchers from the University of Aalborg who have done earlier work
with Lauritzen.
Large Bayesian networks can be intractable to interpret exactly when
there are sets of interdependent nodes that collectively define a very
large state space. In cases like this approximate techniques can be
used to provide a solution. Pearl [93] developed an
approach to doing this that uses stochastic simulation to determine
the node posterior probabilities. This is a Monte Carlo method in
which during each iteration, random values are selected for each node
from the distribution of values based on the current parent
configuration for the node. This iterative process is similar to the
data augmentation used by Bruce and Wiebe [23].
At the end of the simulation, the relative frequency of the times that
the node has each value defines it's posterior probability
distribution.
Charniak and Goldman [28] describe how
Bayesian networks can be applied to plan recognition. They show how
this is a more natural approach that previous ones, because of the
uncertainty involved in ascribing plans to people.
The main contribution of the paper is the application of Bayesian
Networks to natural language processing.
An additional contribution of the paper is a description of how
knowledge encoded in traditional knowledge representation languages
can be converted into a Bayesian network. This is illustrated with
examples from earlier work in abductive reasoning (e.g., the liquor
store robbery scenario). One drawback of the approach is that it
relies solely on ``explaining away'' of evidence among competing
hypotheses. For instance, there is no mechanism for negative evidence
or the influence of higher-level plans (e.g., be a good citizen).


Next: Other methods
Up: Statistical Inference
Previous: Statistical Inference
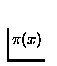 ), potentially influenced by
other children of the parents. The other component is the influence
from the node's childrens (
), potentially influenced by
other children of the parents. The other component is the influence
from the node's childrens (
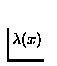 ). By separating these
components, belief propagation can be done locally without introducing
instabilities (e.g., counting evidence twice).
). By separating these
components, belief propagation can be done locally without introducing
instabilities (e.g., counting evidence twice).