

This figure represents 3+1. After the addition, the tape will contain:

This assumes a destructive algorithm; S and
E markers have been inserted in the process of the
algorithm, and have not been removed.
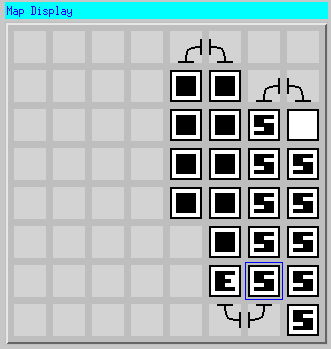
Our optional problem implements a destructive Turing Machine algorithm for unary addition.
T junctions (entered from the left). Since we only
have limited map area, we use curved tiles to turn the robot and keep
it on the map; they have no meaning in the encoding. An example
problem, adding 4+5 using this encoding, is shown:


to leave behind a start-of-number marker and enters state
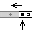
The robot will stay in this state for as long as it encounters
Ts.
Each of these are identified on the map with

When it reaches the end of the first block of numbers, it enters state
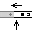
and marks the tile with

to identify it as a space. It marks the tiles in the second block like those in the first. After marking the second block, it marks a tile with

to mark the end of the input. At this point, parsing is complete.
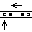
and drives to the left of the center line so all of the sensors will be in a known state (note: when this happens, it looks like the robot has gotten lost).
Using state
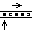
tiles back to the end-of-number marker are traversed, and a new end-of-number marker is written. The head is moved to the end of the sum, a mark written, and the robot moved one square, using the same approach.
The complete robot and tile state sets are:

and