


Next: About this document ...
Up: No Title
Previous: Question 2
The intuition is that negation for finite goals can be implemented in
this case by computing the set of all the solutions and then checking
membership. For a ground goal
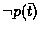 , having a finite derivation
tree, we have:
, having a finite derivation
tree, we have:
where the intensional set construction on the right can be directly
expressed using the complete implementation of setof available in the
assumption of the problem.
Chito
1999-07-06
![]() , having a finite derivation
tree, we have:
, having a finite derivation
tree, we have: