Question 2

(i)

The basic idea is to build a finite automaton that simulates in an alternating fashion the steps of automata accepting L₁ and L₂.

Let $M_1=(Q_1,\Sigma, \delta_1, s_1, F_1)$ be a DFA that accepts L₁ and $M_2=(Q_2,\Sigma, \delta_2, s_2, F_2)$ be a DFA that accepts L₂. Construct the automata $M_3=(Q_3, \Sigma, \delta_3, s_3, F_3)$ as follows:

$Q_3 = Q_1 \times Q_2 \times \{ 1,2 \}$

s₃ = (s₁,s₂,1)

$F_3 = F_1 \times F_2 \times \{ 1 \}$

and for all $(q,p,l) \in Q_3$ and for all $a \in \Sigma$,

$\delta_3((q,p,l), a) = \left \{ \begin{array}{ll} (\delta_1(q,a),p,2) \,\,\,\,... ...\\ (q,\delta_2(p,a),1) \,\,\,\,{\mbox \,\, if\,\, } l=2 \end{array} \right .$

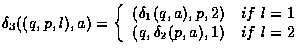
Then one can easily show that $L(M_3) = L_1 \diamond L_2$. Hence, $L_1 \diamond L_2$ is regular.

Note: It would be nice if the answer includes a proof of $L(M_3) = L_1 \diamond L_2$ but the construction would be enough.

(ii)

We first show that $A \diamond B = \{ a^{4p}(ab)^pb^{6p}\,\,\vert\,\,p \geq 0 \}$.

Clearly, for all $p \geq 0$, $a^{4p}(ab)^pb^{6p} \in A \diamond B$ as $a^{4p}(ab)^pb^{6p} = a^{3p}b^{3p} \diamond a^{2p}b^{4p}$ and $a^{3p}b^{3p} \in A$ and $a^{2p}b^{4p} \in B$. Hence,

$\{ a^{4p}(ab)^pb^{6p}\,\,\vert\,\,p \geq 0 \} \subseteq A \diamond B$.

Let $x \in A \diamond B$. Then $x=u \diamond v$ for some $u \in A$ and some $v \in B$ with |u|=|v|. Since all strings in A have even length it follows that |u| is even. Since all strings B have length divisible by 3 it follows that |v| is divisible by 3. Since |u|=|v| it then follows that |u|,|v| are divisible by 6. Therefore |u|=|v|=6p for some p. The only string in A of length 6p is a^3pb^3p. The only string in B of length 6p is a^2pb^4p. Hence, $x=a^{3p}b^{3p} \diamond a^{2p}b^{4p} = a^{4p}(ab)^pb^{6p}$. Hence,

$A \diamond B \subseteq \{ a^{4p}(ab)^pb^{6p}\,\,\vert\,\,p \geq 0 \}$.

Therefore, $A \diamond B = \{ a^{4p}(ab)^pb^{6p}\,\,\vert\,\,p \geq 0 \}$.

We now show that $L = \{ a^{4p}(ab)^pb^{6p}\,\,\vert\,\,p \geq 0 \}$ is not a CFL. Assume, to the contrary, that L is a CFL. Then the pumping lemma for CFL's holds for L. Let l be the pumping constant. Now consider the string

s = a^4l(ab)^lb^6l.

Clearly, $s \in L$ and $\vert s\vert \geq l$. Then by the pumping lemma there exists a split of s = uvwxy satisfying

1.

$\vert vx\vert \geq 1$

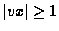
2.

$\vert vwx\vert \leq l$

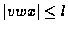
3.

$\forall{i\,\,} uv^iwx^iy \in L$.

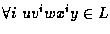We show that this is not the case by considering all possible splits of s. This will yield a contradiction hence showing that the pumping lemma for CFL's does not hold for L and hence L is not CFL.

We claim that for all possible splits uvwxy of s satisfying conditions 1 and 2 above, $uv^0wx^0y \not \in L$. Recalling that $\vert vwx\vert \leq l$ we have the folllowing cases:

Case 1: vwx lies completely within a^4l. In this case, $uv^0wx^0y = a^{4p-\vert vx\vert}(ab)^lb^{6l} \not \in L$ as $\vert vx\vert \geq 1$.

Case 2: vwx lies completely within (ab)^l. Similar to case 1.

Case 3: vwx lies completely within b^6l. Similar to case 1.

Case 4: vwx lies in the part a^4l(ab)^l but not within a^4l or (ab)^l individually. Since $\vert vx\vert \geq 1$ either $\vert v\vert \geq 1$ or $\vert x\vert \geq 1$. If $\vert v\vert \geq 1$ then certainly a non-empty part of v lies within a^4l (else vwx lies totally in (ab)^l). Then uv⁰wx⁰y = a^4l-tzb^6l where $t \geq 1$ and z = (ab)^j or z=b(ab)^j for some $j \leq l$. In either case, $uv^0wx^0y \not \in L$. The case where $\vert x\vert \geq 1$ is similar.

Case 5: vwx lies in the part (ab)^lb^6l but not within b^6l or (ab)^l individually. An argument similar to case 4 shows that $uv^0wx^0y \not \in L$.