
(photo from http://www2.cruzio.com/~vagabond/ComptHome.html)
Here's another problem: we only have fixed-length registers in a computer. In the case of the hc11, the registers that we use for arithmetic (the A register, which you've seen before, and the B register, which is new) are only 8 bits wide. So what happens if we add something like
a3
+b4?
The main thing is, we get a result that won't fit. The fix for this is to always do modulo arithmetic: so any arithmetic operation using an 8 bit register is performed mod 256. We can actually turn this problem to our advantage, if we're clever about it.
This isn't the only place we run into similar problems: one of my favorite examples is automobile odometers. Everybody knows that a used car with fewer miles on the odometer is, all things considered equal, worth more than one with more miles. So, unscrupulous used-car sellers would hook up a drill to the input of a speedometer head, and run the speedometer backwards for a few thousand miles. This subtracts mileage from (the normal term is "rolls back" the odometer, and makes the car worth more money. It's also punishable as fraud, of course.
Well, more modern cars have odometers that won't roll back. Not to worry; if you just roll the odometer forward far enough, you get the same effect. Suppose you have a car with a 100,000 mile odometer, currently showing 87,000 miles. If you run the odometer forward 80,000 miles it'll run up to 99,999 miles and roll over to 0, and then run up to 67,000 miles.
Now here is the important thing: there is no real way of telling the difference between an odometer that's been rolled back 20,000 miles, and one that's been rolled forward 80,000 miles. In a very real sense, in "odometer arithmetic," adding 80,000 is the same thing as subtracting 20,000. We're going to use this to get a representation for negative numbers.
There have also been mechanical calculators which make use of the same principle for handling subtraction; my favorite example is the "Comptometer," which was invented by Dorr Eugene Felt and patented in 1887. A very good page describing comptometers is at http://www2.cruzio.com/~vagabond/ComptHome.html.
A comptometer had several columns of keys, as shown in this photograph of a Wood-cased Comptometer (the earliest commercial model).

(photo from http://www2.cruzio.com/~vagabond/ComptHome.html)
Each key had a number on it; when you pressed the key it would rotate the wheel at the front of the column by the appropriate amount. So, for instance, if you pushed "5" and then "3", "8" would appear in the window. The machine was able to perform carries as appropriate between columns.
In the previous paragraph, I said that each buton was labelled with a number. That wasn't quite true: each key actually had two numbers on it: a number in a large typeface, which worked like I just said, and a second number in a smaller typeface which was the difference between nine and the large number (so the "5" key also had a small "4", and the "8" key also had a small "1"). These little numbers were used to do subtraction: to subtract a number, you would
It turns out that this worked just like running the odometer forward to roll it back.
There's a simulation of a comptometer, written in Java, at http://www.webcom.com/calc/applets/felt/welcome.html You can use that to try to get a feel for what it was like to use a Comptometer.
In order to fit this example on the blackboard, let's assume 3 bit numbers, so we have the numbers 0 through 7 and all arithmetic is mod 8.
Let's make a number line. Unfortunately, since 0 has to follow 7, it can't be a line; it has to be a circle. Now, adding goes clockwise on the circle, and subtracting goes counterclockwise. Here's a picture of the number circle, showing the circle, the numbers on it in decimal, the same numbers in binary, and which direction to go for addition and subtraction.
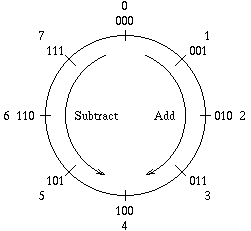
Question: If I go from 3 to 1, can you tell whether I did it by subtracting 2, or by adding 6? Well, no you can't. Now, here's an idea: any time we want to subtract some number n, we can instead add (8-n). And that means that the way we represent a negative number -n is by using (8-n) instead.
We'll let the lower half of the numbers represent themselves, and the upper half represent negative numbers. That means we can tell a positive number from a negative number by the most significant bit: we'll call this the Sign Bit. So now it looks like this:
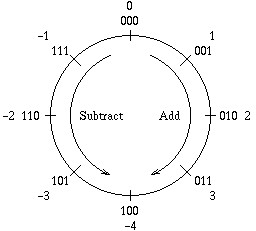
One last wrinkle: if we have to subtract and negate by taking 8-n, we haven't bought ourselves anything: we still have to subtract. But remember that 8-n = (7-n)+1. And 7-n can be calculated easily! We can just negate every bit!
| Old | New | Digit |
|---|---|---|
| 97 | 6 | 1 |
| 6 | 0 | 6 |
1 with a
0, and every 0 with a 1.
Working in hexadecimal, this is equivalent to subtracting every digit
from f. Since we're assuming a 16 bit word, we need to
subtract from ffff (you actually need to subtract from
enough f's to fill out the word. If it were a 32 bit
word, we'd need ffffffff).
ffff - 0061 = ff9e.
ff9e + 1 = ff9f.
00100001.
00100010.
| Old | Bit | New |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 2 | 0 | 2 |
| 4 | 0 | 4 |
| 8 | 0 | 8 |
| 16 | 1 | 17 |
| 34 | 0 | 34 |
Here's another problem: if we solve the problem of results that are too big by throwing away the carry, how do we know what happened? An answer that's common to many computer architectures is to have an extra register, which gets values assigned to it as a side-effect of other instructions. If we need to, we can look at this register to figure out what happened.
In the HC11, this register is called the Condition Code register. There are four bits in it, which are the same four bits used in just about every architecture, as follows:
| 2 | f | 6 | a |
| +2 | +f | +6 | +a |
| 4 | e | c | 4 |
| V = 0 | V = 0 | V = 1 | V = 1 |
| C = 0 | C = 1 | C = 0 | C = 1 |
One last thing about the CCR is that it's really eight bits, not four. It's going to turn out that we'll be using it to keep track of, and control, more than just the four condition code bits we've talked about so far.
It's impossible to have a carry-out if we add two values together whose sign bits are 0. We will always have a carry-out if we add two values together whose sign bits are 1. If we add two numbers together, one of whose sign bits is 1 (and the other is 0), we will get a carry-out if the result's sign bit is 0 and no carry-out if it's 1.
It's impossible to have an overflow if we add two values together with different sign bits. If we add to numbers together with the same sign, and the result is the opposite sign, we will get an overflow.
We've spent enough time on signed numbers that it's important to step back a bit and remember something: just as the only difference between instructions and data is how we want to interpret the bit field, the only difference between a signed and an unsigned value is how we want to interpret it. It's really easy to get confused if you're not careful! A few comments:
This will be important when we're doing conditionals.
Some examples:
1316 + 4a16 = 5d16. In decimal, this is 19 + 22 = 41, which is correct whether we want to interpret the numbers as signed or unsigned.
8916 + 7f16 = 0816. The C bit will be 1; the V bit will be 0. If regard these as signed numbers and convert them to decimal, we get -119 + 127 = 8, which is correct. But if regard them as unsigned, we get 137 + 127 = 8, which is wrong. But, just in case you get the idea that interpreting the numbers as signed is correct and unsigned is incorrect...
...7316 + 2b16 = 9e16. The C bit will be 0; the V bit will be 1. If we regard those numbers as unsigned and convert to decimal, this is 115 + 43 = 158, which is correct. But... if it's signed, it turns into 115 + 43 = -98, which is wrong!
To summarize, the numbers are just numbers. We can interpret them as either signed or unsigned. There are combinations that end up being correct when we interpret them as unsigned but wrong as signed, and vice versa. In all these cases, the condition code bits contain enough information to tell us what happened (and to reconstruct the correct result if we really need it).